 一般運動量
一般運動量 相対論的ラグランジアン
相対論的ラグランジアン《はじめに》
ランダウ・リフシッツの「力学」から、最小作用の原理とラグランジアンを学んだ。次は、「場の古典論」が、最小作用の原理を用いて相対性原理のラグランジアンを設定して電磁気学のマックスウェルの方程式を導き出すことを学ぶ。
この内容は、大学の理論物理学の中でも、かなり難しい部分になります。
【教科書の紹介】
先ず、ランダウ・リフシッツの「場の古典論」を紹介します。
場の古典論(原書第6版) (ランダウ=リフシッツ理論物理学教程) 単行本 – 2022/5/26
エリ・デ・ランダウ (著), イェ・エム・リフシッツ (著),
恒藤 敏彦 (翻訳), 他
内容
相対性原理
相対論的力学
場のなかの電荷
場の方程式
不変な場
電磁波
光の伝播
運動している電荷の場
電磁波の放射
重力場のなかの粒子
重力場の方程式
物体の重力場
重力波
相対論的宇宙論
【第1章】相対性原理
《第6節》4元ベクトル
事象の座標としてx,y,z,τ=ict を用いるならば、x,y,z,τ=ict を4次元空間のベクトルの成分とみることができる(第2版では、時間成分を虚数であらわしていた)。これらの成分の2乗の和、

は、ローレンツ変換を特殊な場合として含む4次元座標系の回転によって変化しない。
(「場の古典論」の第2版では)x,y,z,τ=ict を成分とする以下のベクトルが、動径4元ベクトルとよばれる。

以上のように4元ベクトルの時間成分を虚数であらわす(第2版の)流儀の他に、4元ベクトルの時間成分を実数のw=ct であらわす流儀がある。その流儀では、以下の形で4元ベクトルをあらわす。

「場の古典論」の第6版では、その流儀を採用し、更に進めた表記方法で、以下の形で4元ベクトルをあらわす。

第6版では、動径4元ベクトルの長さの2乗を以下の式で定義している。

慣性基準系の静止系K(ct,x,y,z)とそれに対してx軸方向へ速度vで運動している慣性基準系K'(ct',x',y',z')の間では、動径4元ベクトルの成分は、つぎのようにローレンツ変換される。
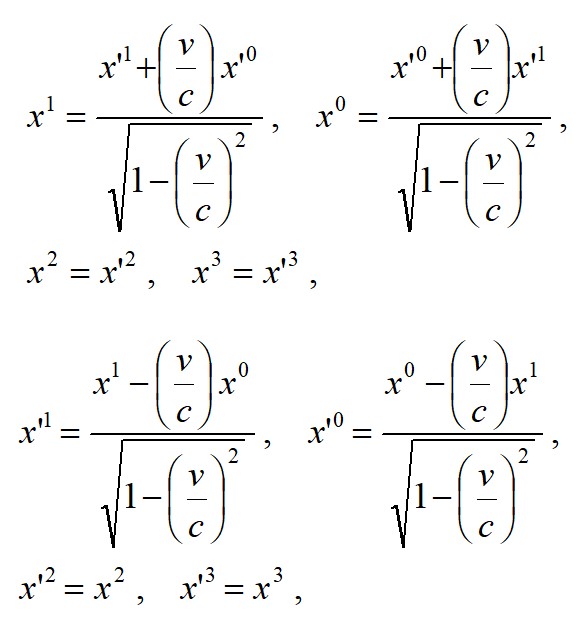
4次元座標系のローレンツ変換によって動径4元ベクトルの成分と同じように変換される4つの量、

の総体を4元ベクトルAi とよぶ。
4元ベクトルの長さの2乗は、動径4元ベクトルの長さの2乗と同様に、以下の式で定義する。

《反変ベクトルと共変ベクトル》
ローレンツ変換によって、座標のように変換される4元ベクトルは反変ベクトルである。
一方で、ローレンツ変換によって異なる変換をする共変ベクトルがある。スカラー量を座標成分や時間成分で偏微分して作るベクトルが共変ベクトルである。
4元ベクトルである反変ベクトルの空間成分を逆符号に反転してやると、共変ベクトルに変わる。
4元ベクトルAi に対応する共変ベクトルを以下の記号であらわす。

共変ベクトルの成分は、反変ベクトルの成分との間に以下の関係がある。

そうすると4元ベクトルの2乗は、

とあらわせる。
《アインシュタインの縮約記法》
われわれは、このベクトルの内積をAiAi と記し、一般に2度くり返して現れるラテン添字については、0から3まで和をとるものと約束する(アインシュタインの縮約記法)。

4元ベクトルの2乗と同様にして、2つの異なる4元ベクトルのスカラー積が作られる。

積 AiBi は4元スカラーである。すなわち、その値はローレンツ変換によって変わらない不変量のスカラーである。
《計量テンソル》
反変ベクトルと共変ベクトルを相互に変換する計量テンソル gik=gik を導入する。

この計量テンソルを使って、以下のように反変ベクトルを共変ベクトルに変換し、また、その逆の変換をする。


「場の古典論」の§2では、動径4元ベクトルの2乗がローレンツ変換しても不変である4元スカラーであることを利用して、2つの事象の間の間隔をあらわす世界間隔dsを以下の式で定義している。なお、物質粒子のなかで起こる事象は、その粒子の3つの空間座標および事象の起こった時刻によって定義される。

この世界間隔dsは、ローレンツ変換しても不変である。
また、おのおのの粒子に、その粒子が存在する位置の3つの空間座標と時間の点の集合からなる曲線が対応する。その曲線を世界線と呼び、その線上の点を世界点と呼ぶ。一様な直線運動をする粒子には、まっすぐな世界線が対応する。
(注意)記号τを使って、世界間隔ds=dτと定義して使う場合もある。
固有時間
「場の古典論」の第3節では、
速度vで動いている時計の時間経過dt’が、静止した観測者の時計の時間経過dtで、以下の式で表される。

与えられた対象といっしょに動く時計がdt’刻みで経過する時間t’を、この対象の固有時間と言う。
《第6節の続き》4元テンソル
2階の4元テンソルとは、ローレンツ変換によって、座標の積(内積ではない)のように変換される16個の成分の行列のことを、2階の4元テンソルと呼ぶ。
(4元テンソルには、4元ベクトルとは異なるローレンツ変換での不変量がある。)
《極性ベクトルと軸性ベクトル》
正規基底ベクトルの方向を逆向きにすることで空間座標系を反転すると、3つの3次元座標すべての符号が逆になる。それにより、正規基底ベクトルと座標成分の積で合成される通常の空間ベクトルは変わらない。そういう空間ベクトルを極性ベクトルと呼ぶ。
一方で、3次元ベクトルの外積は、正規基底ベクトルの方向を逆向きにすると、3つの3次元座標すべての符号が逆になるが、外積の成分の符号は変わらない。そのため、正規基底ベクトルと座標成分の積で合成されるベクトルの方向が逆向きになる。そういう空間ベクトルを軸性ベクトル(擬ベクトル)と呼ぶ。
《擬スカラー》
擬スカラー とは、座標系の取り方を右手系⇔左手系と変えると,その符号を変えるスカラーのことである。
【問題2】
反対称な4元テンソルの成分の変換則を求めよ。

この反対称な4元テンソルの成分の変換則の解。

《第7節》
通常の3次元の速度ベクトルから4次元ベクトルを作ることができる。粒子の4次元的な速度(4元速度)とは、ベクトル

である。
これらの成分を見いだすために、

であることに注意する。ただし、vは粒子の3次元的な速度である。粒子はx方向に速度vxで進むものとする。こうして、以下の式を得る。

(注意)4元速度はローレンツ変換によって座標系と同様に変換される4元ベクトルである。一方、通常の3次元速度ベクトルは4元ベクトルではない。慣性基準系が異なる観測者が観測する3次元速度のローレンツ変換の式は第5節で述べた通りである。
4元速度uiは以下の式であらわされる。

である。したがって、ui は単位4元ベクトルであって、運動する粒子の慣性基準系からみたら時間成分のみを持つベクトルである。4元速度ベクトルui の長さの2乗の値はローレンツ変換によって変わらない不変量の値1である。なお、4元速度ui は、運動する粒子の慣性基準系から観測すると、時間成分のみを持つ4元ベクトルである。
《4元加速度》
4元加速度を以下の式で定義する。

4元加速度も4元速度と同様にローレンツ変換によって座標系と同様に変換される4元ベクトルである。
4元加速度と4元速度の内積は0である。
なお、4元加速度を具体的にあらわす式は簡単ではなく、以下の式で計算できる。


4元加速度ωi は、運動する粒子の慣性基準系から見たら空間成分のみを持つ4元ベクトルであり、時間成分のみを持つ4元速度ui と直交する。3次元加速度は4元ベクトルではないが、上記の式のように4元加速度の式の中に組み込まれている。速度vが光速度より十分に小さい場合は、3次元加速度は近似的に4元加速度の空間成分掛けるcの2乗倍になり、その誤差の割合は(v/c)の2乗のオーダーになる。4元加速度の時間成分の大きさは、空間成分に対する比が(v/c)のオーダーで小さい。4元加速度はローレンツ変換によって動径4元ベクトルと同じ形で変換される。速度vが光速度より十分小さい場合の4元加速度のローレンツ変換では、4元加速度の空間成分の変化の割合は(v/c)の2乗のオーダーで小さい。そのため、3次元加速度の、ローレンツ変換による変化の割合が、(v/c)の2乗のオーダーで小さい。
【リンク】
「高校物理の目次」
0 件のコメント:
コメントを投稿